7. hét: rekurzió

Felkészülés a laborra:

• A rekurzióról szóló előadás áttekintése.
• A nyomkövetésről tanultak átismétlése.

Tanultad, hogy egy n szám faktoriálisát így is lehet definiálni:

     ┌
     │ 1,        ha n = 0
n! = ┤
     │ n·(n-1)!, ha n > 0
     └

Fogj egy papírlapot, és fejtsd ki n! értékét kézzel, az alábbi módon! Vagyis helyettesítsd be a faktoriális definíciója szerint megadott szabály szerint a kifejezést.

6! = 6 * 5!
   = 6 * 5 * 4!
   ...

Ha ezzel megvagy, írj Python programot, amely egy rekurzív faktoriális függvényt tartalmaz! Vagyis térjen ez vissza 1-gyel, ha a paramétere 0, és n * fakt(n-1)-gyel, ha nagyobb. Teszteld a megírt függvényed, írd vele ki a faktoriálisok értékét 0-tól 10-ig!

0! = 1
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
10! = 3628800

Vigyázz: rekurzív függvényt kell írnod, ebben nem kell ciklus, se while, se for. Változó sem lesz benne. A main()-ben viszont lehet.

def fakt(n):
    if n == 0:
        return 1
    else:
        return n * fakt(n - 1)

def main():
    for i in range(0, 10+1):
        print(f"{i}! = {fakt(i)}")

main()

Engedélyezd most a nyomkövetést a laboron tanult módon. Figyeld meg, hogyan hívja a függvény saját magát a fakt(6) kifejezés kiértékelése közben. Az IDLE nyomkövető az ablak felső részében mutatja a függvényhívásokat:

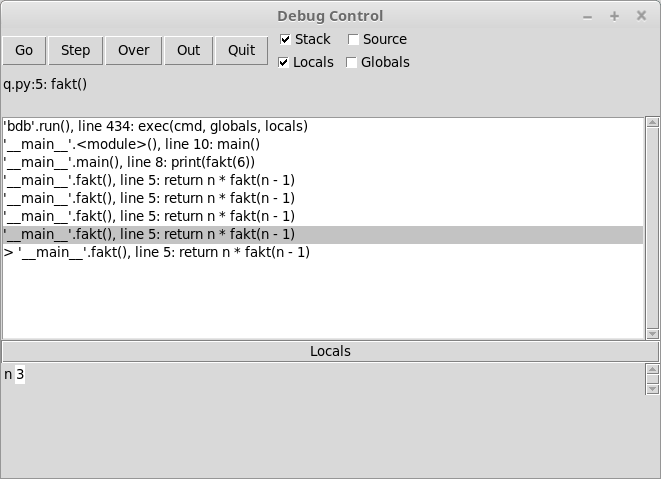
Az egyes hívásokra kattintva alul látszik, hogy azokhoz milyen paraméter tartozik.

Tanulmányozd az alábbi rajzot!

A legfelső sorban egy szimpla vonalat látsz. Képzeld azt, hogy a szimpla vonalat 3 egyenlő hosszúságú darabra töröd (ahol a jelek vannak), és a középső részt egy 60 fokos háromszöggel helyettesíted. Vagyis megteszed az 1/3 hosszt, aztán balra fordulsz 60 fokot, újabb 1/3, jobbra fordulás, újabb 1/3, és végül balra fordulás, befejező 1/3. Így alakult ki a második rajz. Ha a második rajz összes szakaszát helyettesíted saját magával, akkor jutsz a harmadik rajzhoz.

Egy olyan rekurzív függvényt kell írnod, amely ezt a rajzot elkészíti teknőcgrafikával. A gondolatmenet a következő:

• A függvény paraméterként kap egy hosszt (h), és a rajz bonyolultságát (n).
• Ha a legegyszerűbb esetet kell megrajzolni (n = 0), akkor csak húz egy egyenes szakaszt.
• Ha egy bonyolultabb esetet, akkor pedig bejárja a szakasz-fordulás-szakasz-fordulás-szakasz-fordulás-szakasz útvonalat, megrajzolva ezt a formát: _/\_.
• Ahol viszont szakaszt kell rajzolnia, oda nem szakaszt rajzol, hanem az eggyel egyszerűbb ábrát: n-1.

Előbb készítsd el azt a változatot, amelyik csak a középső ábrát rajzolja ki, utána egyszerű a szakaszok rajzolását rekurzív hívásra cserélni!

Rajzolj hópelyhet az előző feladat fraktáljával! Ehhez nincs más dolgod, mint három fraktált egymás mellé tenni, egymáshoz képest 120 fokkal elforgatva (lásd a bal felső rajzot). Minél nagyobb a bonyolultság, annál szebb lesz a hópehely.

Valósítsd meg ezt egy hopehely(hossz, bonyolultság) paraméterű függvényben! Használd fel ehhez az előző fraktál függvényt, változatlan formában!

import turtle
 
def fraktal(h, n):
    if n == 0:
        turtle.forward(h)
    else:
        fraktal(h / 3, n - 1)
        turtle.left(60)
        fraktal(h / 3, n - 1)
        turtle.right(120)
        fraktal(h / 3, n - 1)
        turtle.left(60)
        fraktal(h / 3, n - 1)
 
def hopehely(h, n):
    for _ in range(3):
        fraktal(h, n)
        turtle.right(120)
 
def main():
    turtle.speed(0)
    hopehely(300, 4)
    turtle.done()
 
main()

Egy számtani sorozatot (jelöljük most S-sel) annak első tagjával és növekményével definiáljuk. Az első tag S0 értéke a, a többi tagot pedig úgy számítjuk ki, hogy mindig az előző taghoz hozzáadjuk d-t, a növekményt:

     ┌
     │ a,        ha i = 0
Si = ┤
     │ Si-1 + d, ha i > 0
     └

Írj rekurzív függvényt, amelyik megkapja 1) a sorozat első tagját: a, 2) a sorozat növekményét: d, és 3) hogy a sorozat hányadik elemét kell megadja: i, és visszatér Si értékével! Alkalmazd a függvény megírásakor a fenti rekurzív definíciót! Egészítsd ki a megírt függvényt egy főprogrammal, amelyben kiírod egy számtani sorozat első 10 elemét!

A főprogramban lehet ciklus, de a sorozatot megadó függvényben ne legyen se while, se pedig for!

def szamtani(a, d, n):
    if n == 0:
        return a
    else:
        return szamtani(a, d, n-1) + d

def main():
    for i in range(0, 10):
        print(szamtani(5, 3, i))

main()

A hatványozás elvégezhető annál gyorsabban is, mintha a kitevőnek megfelelő számú szorzást csinálnánk. Pl. a8 = a4·a4, a4 = a2·a2 és a2 = a·a miatt a nyolcadikra hatványozáshoz mindössze három szorzásra van szükség. A következő megfigyelést tehetjük:

     ┌
     │ (a·a)k/2, ha k páros
ak = ┤
     │ a·ak-1, ha k páratlan.
     └

Írj rekurzív függvényt, amely a fentiek alapján végzi el a hatványozást! Paraméterei legyenek az alap és a kitevő, visszatérési értéke pedig a hatvány. Írd ki kettő első tizenhat hatványát!

A rekurzív függvénybe most se tegyél ciklust, dolgozz a definíció alapján! Ahhoz, hogy ez működjön, még egy báziskritériumot be kell vezetned, amit a fenti definíció nem tartalmaz. Mi lehet az?

def gyorshatvany(a, k):
    if k == 0:
        return 1
    if k % 2 == 0:
        return gyorshatvany(a * a, k // 2)
    else:
        return a * gyorshatvany(a, k - 1)

def main():
    for k in range(0, 16):
        print(gyorshatvany(2, k))

main()

Írj függvényt, amely paraméterként kap egy pozitív egész számot valamint egy számrendszert, és kiírja a képernyőre a számot a megadott számrendszerben! Elég most, ha csak 10-es számrendszerig működik. A megoldáshoz használj rekurziót! Miért sokkal egyszerűbb ez a megoldás, mint az iteratív?

Írj függvényt, amely a paraméterként kapott pozitív egész számot három számjegyenként csoportosított formában írja ki. Pl.: 16 077 216. Próbáld ki más számokra is: 999, 1000, 12, 0, 1000222!

Hányféleképpen lehet egy adott hosszúságú járdát kikövezni 1 és 2 méter hosszúságú járdalapokkal? Például ha 3 méteres a járda, a lehetőségek: 1+1+1, 1+2, 2+1, tehát összesen 3.

def jarda(hossz):
    if hossz < 0:
        return 0    # lehetetlen
    if hossz == 0:
        return 1    # nem csinálunk semmit
    
    return jarda(hossz - 1) + jarda(hossz - 2)

Ha a laborfeladatokkal elkészültél, dolgozz a példatárban lévő feladatokon, a szorgalmi feladatokon, a minta vizsgán, vagy a házi feladatodon.

Informatikusok próbálják lekódolni az Algoritmusok és gráfok tárgyon tanult algoritmusokat. Ezzel két legyet lehet ütni egy csapásra, mert két tantárgyat is gyakoroltok egyszerre.