Alice in Wonderland
Írj programot, ami halmaz (set) segítségével, megszámolja, hogy hány különböző szó található a szövegben! Teszteld a programot szabadon elérhető hosszabb szövegeken, mint pl. Alice csodaországban. (angol nyelven érdemes kipróbálni)
Módosítsd a programot úgy, hogy szótár segítségével szótár (dict) mindenfajta statisztikát készítsen el, ami elképzelhető: a betűk és írásjelek előfordulását, a szavak előfordulását, a mondatok átlagos hosszát, stb.
Minta házi feladat
Alakítsd át úgy a minta házi feladatot, hogy Python halmazt és halmazműveleteket használjon!
Konyha
Egy konyhán különféle ételeket készítenek. Van egy raktáruk, rengeteg élelmiszerrel, és adott többféle étel receptje, amiből most a hozzávalók listája érdekes csak.
A raktárkészletet egy Python szótár tartja nyilván (dict). Ebben a kulcs az élelmiszer neve, az érték pedig a rendelkezésre álló mennyiség. Például: liszt: 6, paprika: 3, tojás: 5, só: 1. Egy konkrét recepthez a hozzávalók szintén egy szótárban tárolhatóak, pl. nokedlihez liszt: 0.4, tojás: 1 stb. Ezekhez tartozna mértékegység is (liszt: kg, tojás: db és így tovább), de ezeket elhagyjuk, nem lényegesek most.
Írj függvényt, amelyik egy étel elkészítését kezeli! Vegye át ez paraméterként a készletet és a hozzávalókat, továbbá egy mennyiséget, hogy hány adagot kell főzni (ennyivel kell megszorozni az egyes hozzávalókat). Ha van minden hozzávalóból elég, akkor vonja le a függvény a készletből a felhasznált élelmiszereket, és adjon igazat. Ha bármelyikből hiány van, vagy egyáltalán nincs olyan hozzávaló, akkor ne csináljon semmit, hanem adjon hamisat! (Mivel felesleges belekezdeni a főzésbe, ha nincs mindenből elegendő.)
Írj függvényt, amelyik fájlba írja a paraméterként adott raktárkészletet! Minden tételhez a fájl egy sora tartozzon. A sorok elején legyen a mennyiség, utána pedig az élelmiszer neve, vesszővel elválasztva.
Írj függvényt, amelyik a paraméterként megadott nevű fájlból beolvas egy teljes raktárkészletet, és visszaadja azt!
Statisztika szótárral
Ebben a szövegfájlban egész számok találhatók, soronként egy darab. Készíts programot, amely szótár (dict) használatával statisztikát készít, azaz megszámolja, hogy a parancssori argumentumként megadott fájlban melyik egész szám hány százalékban fordult elő. Ha nincs parancssorban fájl megadva, adjon hibajelzést! A beolvasás legyen hibabiztos, az egész számként nem értelmezhető bemenetet a program hagyja figyelmen kívül!
Az eredményt hisztogramként, a példához hasonlóan ábrázold! (tipp: a leggyakoribb számhoz tartozó oszlop legyen 50 karakter széles)
statisztika.py adatok.txt
3816: 0.00%
3817: 0.02%
3818: 0.04%
3819: 0.25%
3820: 0.55% #
3821: 1.40% ####
3822: 2.84% #########
3823: 5.00% ################
3824: 8.27% ##########################
3825: 11.87% ######################################
3826: 13.26% ###########################################
3827: 15.38% ##################################################
3828: 11.98% ######################################
3829: 11.25% ####################################
3830: 7.67% ########################
3831: 5.03% ################
3832: 2.70% ########
3833: 1.49% ####
3834: 0.61% #
3835: 0.26%
3836: 0.09%
3837: 0.03%
3838: 0.01%Vigyázz! A dict alapvetően nem rendezve tárolja a kulcsokat, használd a sorted függvényt!
Névnapok
Ez a fájl a névnapokat tartalmazza: (forrás: https://people.inf.elte.hu/csa/nevnap.txt)
01.01 Fruzsina
01.02 Ábel
01.03 Benjámin
01.04 Titusz Leona
01.05 Simon
01.06 Boldizsár
01.07 Attila Ramóna
...Olvassa be ezt a fájlt a beolvas() függvényed! A paramétere legyen a fájlnév, visszatérési értéke pedig egy általa létrehozott
dict objektum. Az utóbbi kulcsai a napok (hónapot és napot, két egész számot tartalmazó tuple), értékei pedig listák, hiszen
egy napon több névnap is lehet. Pl. nevnapok[(1,7)] értéke ["Attila","Ramóna"].
Írj ezután egy másik, megfordit() nevű függvényt, amelyik megfordítja ezt a dict-et! Vagyis hozzon létre egy másikat, amelyet
névvel lehet indexelni, és úgy dátumokat kapunk, hogy mikor vannak az ahhoz tartozó névnapok. Például datumok["Péter"] értéke
[(6,2),(6,29)] lesz a fenti adatokkal. A függvény paramétere az eredeti dict, értéke pedig az új dict legyen.
Írj főprogramot, amelyik beolvassa a nevnapok.txt fájlt az első függvénnyel, megfordítja a másikkal; végül pedig kér egy nevet a felhasználótól, és kiírja, hogy mikor tarthatja a névnapjait! (Vagy hogy nincs olyan név.)
Bejárások
A bináris fák algoritmusait rekurzívan írtuk meg. Alakítsd át ezeket az algoritmusok iteratívvá a sor (deque) segítségével! Készíts szélességi bejárást, amikor a fát szintenként járjuk be! A wikipédián megtalálod ezeknek az algoritmusoknak a pszeudókódjait.
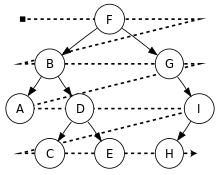
Kifestés
Itt található a rekurzív kifestő algoritmus. Alakítsd át ezt az algoritmust úgy, hogy rekurzió helyett sort használjon!