Megajánlott jegyhez a NEPTUN-ban fel kell venni a december 16-i vizsgát. (több is van, azt kell felvenni, ahol megjegyzésben oda van írva, hogy a megajánlott jegy beírására, nincs létszámkorlát és terem se) Ha megajánlott ötösöd van és ezt nem teszed meg, nem tudjuk beírni a jegyet és elveszik.
Pót-pót ZH-hoz pedig az infopy portálon kell jelentkezni. A pót-pót ZH különeljárási díjas!
Gyakran előfordul, hogy valamilyen változó értékét egymás után sorban kell összehasonlítanunk
és ettől függően más és más kódrészletet kell lefuttatnunk. Python 3.10 előtt erre az
if - elif - else szerkezetet használtuk. Tipikusan állapotgépekben ez a vezérlési szerkezet
nagyon gyakran fordul elő. Pl. az előadáson mutatott kódrészlet, a LY számláló egy részlete az következő:
Az if-elif-else
kígyó...
if c == "l":
allapot = LL_VOLT
elif c == "y":
szaml += 1
allapot = ALAP
else:
allapot = ALAP
...if-elif sor jól olvasható. De egy
nagyobb állapotgép esetén, pl. egy pygame alkalmazásban, ahol "minden" eseményt le kell kezelnünk,
az if-elif-else szerkezet kevésbé olvasható kódhoz vezet.
Más nyelvekben már régóta rendelkezésre áll a többszörös összehasonlítás lehetősége, és ez a 3.10 verzióban
a Python-ba is megérkezett, az ún. match - case szerkezet. ("Jó" Python szokás szerint egy picit hívják
csak másképpen mint a C szintaktikát alkalmazó elterjedt nyelvekben (C, C++, C#, Java, JavaScript stb.) ott ezt
switch - case néven kell keresni. Cserébe viszont többet is tud.)
Használata alapesetben nagyon egyszerű. A match utáni változót hasonlítjuk össze a case-ben leírt esetekkel.
Pl. az előző eset példáját így írhatjuk át. A case ágakba tesszük az összehasonlítandó értékeket, majd utána megfelelő
kódrészletet. Az utolsó case, az aláhúzás speciális: ezzel jelezzük azt, hogyha a felette lévő esetek közül egyik sem
teljesült, akkor minden más értékre ezt kell csinálni.
match mit
case mivel.
match c:
case 'l':
allapot = LL_VOLT
case 'y':
szaml += 1
allapot= ALAP
case _:
allapot= ALAP Lehetőségünk van többszörös eset létrehozására is, az | operátor használatával.
Ez a vagy kapcsolat jelölése.
Például egy 1-10 terjedő szám római kiírása így is írható:
def romai(n):
match n:
case 1 | 2 | 3: return "I"*n
case 4: return "IV"
case 5 | 6 | 7 | 8: return "V" + "I"*(n-5)
case 9: return "IX"
case 10: return "X"
case _: return ""A case-ben nem csak konstans és egész számra visszavezethető, pl. karakter érték (más nyelvek terminológiájával élve integrális típusú) állhat, hanem bármi. Ezek közül a legizgalmasabb a lista vagy a tuple.
parancs= input().split()
match parancs:
case "go", "north":
print("Észak felé")
case "go", "east":
print("Kelet felé")
# ...
case _:
print("Ismeretlen parancs") A matchben is lehet többszörös illeszkedés és az illesztett részt megkaphatjuk paraméterként is az as
használatával. Feldolgozhatjuk a lista/tuple maradék részét a *operátorral és végezetül az alapesetet hívhatjuk other-nek is.
parancs= input().split()
match parancs:
case "go", "north" | "east" | "south" | "west" as irany:
print(f"Going to {irany}")
case "print", *what:
print(*what)
# ...
case other:
print("Ismeretlen parancs")További részletek a kézikönyvben.
Python 3.5 felett megmondhatjuk a paraméterek típusát és a függvények visszatérési értékét. Ezt a futtatáskor a Python SEMMIRE nem használja, de a fejlesztőrendszerek ellenőrzésre igen. Egyrészt tudnak adni segítséget, másrészt a háttérben folyamatosan tudják ellenőrizni a begépelt kódot.
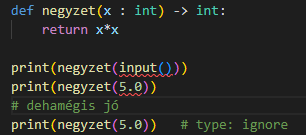
Láthatjuk, hogy ez viszonylag egyszerű. Kettőspont után írjuk a típust, a függvény visszatérési értékét pedig a -> operátor után. Ha ezt megtettük és a fejlesztőrendszerünkben bekapcsoltuk a típusok ellenőrzését, akkor a fejlesztőrendszer figyelmeztetni fog a hibára és kijavíthatjuk, vagy ignorálhatjuk. Ezzel megúszunk olyan bosszantó eseteket, amikor egy elmaradt típus konverzió egy hosszabb futás eredményét esetleg tönkreteszi. Vigyázat, ha bekapcsoljuk lehet, hogy mérgesek leszünk a túlzott precizitástól!
További részletek a kézikönyvben.
Hogyan is működik a for ciklus valójában? Ha írunk egy ilyen sort, mi történik?
for i in range(100):
print(i)Nem fog a Python egy 100 elemű egész tömböt generálni, abban biztosak lehetünk.
it= range(100).__iter__() # vagy iter(range(100))
while True:
try:
print(it.__next__()) # vagy next(it)
except StopIteration:
break Aminek az elemein a for ciklussal végigszaladunk, az egy ún. iterálható (bejárható) objektum. Ennek van két nevezetes
függvénye az __iter__(), ami inicializálja a bejárást és a __next__() , ami mindig a következőt elemet adja, ha
létezik. Az utolsó elem után pedig StopIteration kivételt dob.
Saját magunk is megírhatjuk ezeket a függvényeket. Pl. nézzük meg egy egyszerű láncolt lista esetén:
class ListaIt:
def __init__(self, gyoker):
self.gyoker= gyoker
self.mozgo= gyoker
def __iter__(self):
self.mozgo= self.gyoker
return self
def __next__(self):
if self.mozgo == None:
raise StopIteration
ret= self.mozgo.adat
self.mozgo= self.mozgo.kov
return ret
for e in ListaIt(eleje):
print(e)Láthatjuk, hogy pontosan ugyanazt a függvényt használjuk, mint amit már megírtunk a lista bejárására, de a for ciklus használatával sokkal kifejezőbb és egyszerűbb lett a tároló felhasználása, ráadásul itt sorban kapjuk az értékeket, nem kell magába a bejárást végző függvénybe írnunk az adatfeldolgozást.
Nem minden
iterátor generátor,
de minden generátor
iterátor :-)
A generátorok speciális függvények, amelyek képesek visszatérni egy visszatérési értékkel, de eközben megőrzik saját állapotukat, és
a következő híváskor a végrehajtás onnan folytatódik. Ehhez egy új kulcsszó, a yield tartozik, ezt használjuk a return helyett.
def bejar(eleje):
mozgo= eleje
while mozgo!= None:
ret, mozgo = mozgo.adat, mozgo.kov #
yield ret
for e in bejar(eleje):
print(e)
Belépéskor inicializáljuk a mozgo változót (ez megfelel az __iter__() hívásnak), majd belépünk a ciklusba és a legelső adattal visszatérünk a yield
kulcsszó hatására, de a függvény állapota megőrződik. A következő híváskor a yield után folyatjuk, azaz a while ciklus halad tovább. Ez felel meg a __next__()
hívásnak. Ez egészen addig folytatódik, amíg a függvény végét nem érjük el. Tehát ez valójában egy jóval egyszerűbb szintaxisa az iterátor megvalósításnak.
A legfontosabb előny azonban az, hogy nem kell megvalósítanunk a két különálló függvényt.
További tudnivalókat nézd meg a kézikönyvben.
Egy programban numerikus integrálásokat kell végeznünk különféle függvényekre. Például tudni szeretnénk,
mennyi a math.sin(x) határozott integrálja [a, b] intervallumon, vagy mennyi a negyzet(x)
függvény integrálja [a, b] intervallumon. Ezeket a határozott integrálokat közelíthetjük téglalapok területösszegével:
apró lépésekben kiszámítva mindenhol a függvények értékét, a téglalapok területét, és azok összegét. Fontos megjegyzés: ez az algoritmus
demonstrációs célokat szolgál. Integrált NEM SZABAD ezzel a módszerrel számolni, erre vannak sokkal jobb algoritmusok, kérdezze meg
matematikusát vagy kedvenc keresőjét...
def integral_sin(a, b):
ossz = 0.0
x = a
while x < b:
ossz += math.sin(x) * 0.001
x += 0.001
return ossz
def integral_negyzet(a, b):
ossz = 0.0
x = a
while x < b:
ossz += negyzet(x) * 0.001
x += 0.001
return ossz
def negyzet(x):
return x ** 2Észrevehetjük, hogy lényegében megírtuk kétszer ugyanazt a függvényt. Mindkettőben ugyanaz az
a-tól b-ig menő ciklus van, mindkettő ugyanúgy lép, ugyanúgy kiértékeli a függvényt, ugyanúgy összegzi a
területeket. Az egyetlen különbség a két integráló között az, hogy mely függvénynek az integrálját számítják ki, vagyis hogy mely
függvényt kell meghívni a téglalapok magasságának meghatározásához.
Felmerül a kérdés, hogy nem lehetne valahogy ezt a kódduplikációt megszüntetni? Nem lehetne az integráló függvénynek paraméterként adni azt, hogy mely matematikai függvénynek határoznánk meg az integrálját?
Ha két függvénynek egyforma a fejléce, vagyis egyformán kezelik a paramétereket, akkor kompatibilisek egymással. Az integrálós példánkban minden integrálandó függvény megkap egy számot és elvégez rajta egy műveletet, aminek az eredményét a visszatérési értékben közli.
függvények
def negyzet(x):
return x ** 2
# math.py
def sin(x):
return ...
def harmadikfuggveny(x):
return x - 7 + math.sqrt(x)mint adat
f = negyzet
print(f(3)) # negyzet(3)
f = math.sin
print(f(3)) # math.sin(3)
f = harmadikfuggveny
print(f(3)) # harmadikfuggveny(3)Mi is történik itt? Tegyük fel, hogy van egy függvényünk, amelyik egy darab, szám típusú paramétert vár, és egy darab számot ad vissza. Ha van egy másik függvényünk, amely ugyanígy viselkedik, akkor tulajdonképpen cserélgethetjük őket, egyformán használhatóak. Sőt lehet akár szó saját függvényről is, vagy a Python valamelyik beépített moduljának függvényéről, ennek a működés szempontjából nincs jelentősége.
Ha valamilyen módon egy függvény meghivatkozható, akkor adatként is tudjuk azt kezelni. A fenti kódban ez történik. Az f =
negyzet sorban nem hívjuk meg a függvényt, csak annak hivatkozását betesszük az f nevű változóba. Ha
ezek után az f(3) kifejezést kiértékeljük, az az jelenti, hogy „hívjuk meg a hivatkozott függvényt a 3-as értékű
paraméterrel”. Ha később az f változó egy másik függvényre hivatkozik éppen, akkor ugyanez a kifejezés egy másik
függvény meghívását jelenti.
Mi történik itt a háttérben? A válasz nagyon egyszerű. Mint minden más, a függvény is csak egy objektum, és
annak is lehet referenciája. Az f = negyzet és többi hasonló sor nem csinált mást, elvégezte a szokásos
műveletet: az f változót, mint referenciát, ráállította a függvény típusú objektumra.
Ezek alapján már az integráló függvényünk könnyen parametrizálhatóvá tehető:
import math
def integral(f, a, b):
ossz = 0.0
x = a
while x < b:
ossz += f(x) * 0.001
x += 0.001
return ossz
def negyzet(x):
return x ** 2
def main():
print(integral(negyzet, 5, 10)) # !
print(integral(math.sin, 5, 10))
main()Az integrálónak így három paramétere van: az integrálandó függvény: f, és a határok: [a,
b]. A területek számításánál pedig mindig a paraméterként kapott függvényt hívja, f-et. Ez az f
paraméter a két példában más-más függvénynek referenciája; először a saját negyzet()-ünknek, másodjára pedig a
beépített math.sin()-nek. Mivel ez paraméterré vált, az integráló innentől bármilyen más függvényt is tud integrálni,
lényeg, hogy egyváltozós, valós→valós függvényről legyen szó.
Képzeljük most el, hogy egy határidőnaplós programot írunk. Ebben egy menüből választhatjuk ki a teendőt.
Határidőnapló 1. Adatbevitel 2. Módosítás 3. Keresés 0. Kilépés Melyik?
print("1. Adatbevitel") # 1. sorminta
print("2. Módosítás")
print("3. Keresés")
print("0. Kilépés")valasztas = int(input())
if valasztas < 4:
if valasztas == 1: adatbevitel(esemenyek) # 2. sorminta
elif valasztas == 2: modositas(esemenyek)
elif valasztas == 3: kereses(esemenyek)A sormintákkal mindig az a baj, hogy nehezen módosítható, nehezen karbantartható programkódot eredményeznek. Általában az ilyesmi nem csak azt eredményezi, hogy kódduplikáció van, hanem hogy a kódduplikáció helyei távol vannak egymástól. Ha emitt módosítjuk a kódot, akkor amott is át kell írni valamit.
Tegyük fel, hogy a 2-es menüponthoz szeretnénk beszúrni a törlést. A teendők:
- Beszúrunk egy
print()-et az adatbevitel és a módosítás közé. - Ezek után a többi kiírást is átszámozzuk (módosítás, keresés).
- Az első
if-nél átírjuk a számot 5-re, mert ez a menüpontok számával van összefüggésben. - Beírjuk az
if–elifsorozatba az újvalasztas == 2-t. - Átszámozzuk a többi
if-es sort is.
Ennél biztosan van jobb megoldás is! A sorminta mindig elkerülhető. Például a menüpontok nevei betehetőek listába, és akkor egy ciklussal elvégezhető a kiírás és a beszámozás. Vajon a menüpontok maguk, azaz a függvények is? Ha igen, meg tudjuk szüntetni a második kódduplikációt is!
Vizsgáljuk meg a menüpontok függvényeit!
def adatbevitel(esemenyek):
# ...
esemenyek.append(...)
def modositas(esemenyek):
# ...
esemenyek[i] = ...
def kereses(esemenyek):
for e in esemenyek:
...if valasztas == 1: adatbevitel(esemenyek)
elif valasztas == 2: modositas(esemenyek)
elif valasztas == 3: kereses(esemenyek)Észrevehetjük, hogy itt hasonló a helyzet, mint az előző esetben. Van egy csomó függvényünk, amelyek a menüpontokból kiválasztható tevékenységeket végzik. Ezek mind paraméterként kapják a listát, amelyet aztán módosítanak vagy nem. (Ez a menü szempontjából mindegy, mert a paraméterként átadott lista módosítható a függvényből.) A függvények mindig pontosan egy paramétert kapnak, és nincs visszatérési értékük. Vagyis ezek is kompatibilisek egymással. Ha referenciákat tárolnánk rájuk, akkor létrejöhetne egy függvényeket tartalmazó táblázat, amellyel dolgozhatna a menü!
A függvényobjektumok, és azok referenciái ismeretében a menüpont feliratát és a meghívandó függvényt betehetjük egy objektumba. Ehhez elég egy sima tuple, bár akár definiálhatnánk külön osztályt is.
A menüpontok kiírása és a kiválasztott menüpont végrehajtása:
menupontok = [
("Adatbevitel", adatbevitel),
("Módosítás", modositas),
("Keresés", kereses),
]
# Menü kiírása
for idx, menupont in enumerate(menupontok):
(felirat, _) = menupont
print(f"{idx+1}. {felirat}")
# Választás, és a függvény meghívása
v = int(input())
if 1 <= v <= len(menupontok):
(_, fuggveny) = menupontok[v - 1]
fuggveny(esemenyek)
else:
print("Nincs ilyen menüpont")A felirat és fuggveny változókra nem lenne szükség. De így kicsit érthetőbb a kód,
ha a tuple adatait kicsomagoljuk.
Ezzel a függvényeket a hozzájuk tartozó leírással egy listába tettük. Így az egy új menüpont hozzáadása nagyon egyszerű, csak a listát kell módosítani. A működés automatizált, ha új menüpontunk van, csak kiegészítjük a listát, és minden további programrész helyesen kezeli.
Mivel a függvények adatként kezelhetőek, és paraméterként adhatóak át másik függvényeknek, sok eddig megismert algoritmus működése megfogalmazható általánosságban is. Gondoljunk a programozási tételekre a félév eleji anyagból – ezek mind generikus algoritmusok:
- Számlálás tétele: adott tulajdonságú elemek darabszáma
- Maximumkeresés tétele: legvalamilyenebb elem megkeresése
- …
Ezek a kód szintjén is általánosíthatók, generikusak lehetnek.
számlálás
def szamlal(lista, pred):
db = 0
for x in lista:
if pred(x): # adott tulajdonságú?
db += 1
return dbA program forráskódja is így nagyon szemléletes. Akárhány függvényt írhatunk, amelyek tulajdonságokat vizsgálnak. Ezek a predikátumok:
predikátumok
def negativ(x):
return x < 0
def paros(x):
return x % 2 == 0A függvényeket pedig egyszerűen paraméterként átadjuk:
lista = [5, 7, 12, -6, ………]
print(szamlal(lista, negativ), "db negatív szám.")
print(szamlal(lista, paros), "db páros szám.")A függvény tehát paraméterként kapja a vizsgálandó számsort, továbbá egy másik függvényt, a predikátumot. Ezt a függvényt meghívja minden elemre – ez a függvény mondja meg, hogy az adott elemeket bele kell-e épp számolni, vagy nem. Hogy épp a negatív számok esetén növeljük a számlálót, vagy a páros számok esetén.
Mi a helyzet akkor, ha paraméterezni szeretnénk a predikátumot? Például meg szeretnénk számolni az összes 5-nél nagyobb számot. Vagy 8-nál nagyobbat. 19-nél nagyobbat... Mindegyikhez külön predikátumot kell írni, mert a számlálásban a predikátum egy paraméterű kell legyen?
Szerencsére nem, mert lehetséges függvény belsejében függvényt definiálni:
def szamlal(lista, pred):
db = 0
for x in lista:
if pred(x): # unáris predikátum!
db += 1
return db
def main():
szamok = [ 87, 56, 34, 98, 11, 25 ]
print("Számok:", szamok)
hatar = int(input("Minél nagyobbak? "))
def nagyobb_hatarnal(x):
return x > hatar # !
print(szamlal(szamok, nagyobb_hatarnal), "db")
main()Itt valójában nem csak annyi a lényeg, hogy függvény belsejében van függvény definiálva. Hanem az, hogy a belül definiált
függvény látja a külső függvény lokális változóit. Vegyük észre, hogy a nagyobb_hatarnal() függvény most is
egyparaméterű! Ennek muszáj így lennie, mert a megszámlálás egyparaméterű függvényt vár, unáris predikátumot:
def nagyobb_hatarnal(x):
return x > hatar # hatar = ?Ez a függvény önmagában értelmetlen lenne, mert nincsen benne hatar nevű változó. Azzal válik használhatóvá,
hogy a main()-en belül van definiálva, és annak van viszont van. Tehát az x a predikátum paramétere
(az a legközelebbi x), a hatar pedig az őt becsomagoló függvényét (szintén, ez a legközelebbi
hatar).
Vegyük észre, hogy a megszámlálásnak valójában nem kell tudnia, hogy a predikátum, amit kapott, milyen adatokat lát. Azt az algoritmust csak annyi érdekli, hogy a lista elemeiről megtudja, bele kell-e őket számlálnia vagy nem.
A rendezőalgoritmusokat is meg tudjuk fogalmazni generikusan. Ott ugyanez a helyzet, mint a számlálásnál vagy a keresésnél. Az algoritmus maga ugyanaz, csak az változik, hogy melyik elem kisebb, melyik nagyobb – egész pontosan, hogy melyik való a lista elejére, és melyik a végére, mert kisebbről és nagyobbról itt már nem beszélhetünk.
def rendez(lista, pred):
for i in range(0, len(lista) - 1):
leg = i
for j in range(i + 1, len(lista)):
if pred(lista[j], lista[leg]):
leg = j
temp = lista[i]
lista[i] = lista[leg]
lista[leg] = tempA függvénynek adott predikátum most nem egy-, hanem kétparaméterű. Ugyanis nem egy elemről kell megmondania, hogy rendelkezik-e valamilyen tulajdonsággal, hanem két elemet kell összehasonlítania; előrébb való-e az egyik a rendezett listában, mint a másik. Ha a kisebb elemekre mondjuk azt, hogy előrébb való, akkor növekvő sorrendet kapunk. Ha a nagyobb elemek kerülnek előre, akkor csökkenő lesz a sorrend.
predikátum
def kisebb(a, b):
return a < b
def nagyobb(a, b):
return a > b
lista = [5, 7, 12, -6]
rendez(lista, kisebb) # -6, 5, 7, 12
rendez(lista, nagyobb) # 12, 7, 5, -6Az előző pont egyparaméterű predikátumait unáris predikátumnak nevezzük (unary predicate). Az összehasonlító, kétparaméterű predikátumokat pedig binárisnak (binary predicate).
A list.sort() függvény, illetve a globális sorted() függvény is generikus. Mindkettő
kaphat rendezési relációt, méghozzá a key=... nevű paraméterükben veszik azt át. Ez a két rendezőalgoritmus azonban a
rendezési szempontot másképp kezeli. Nem bináris predikátumot várnak, azaz „kisebb-e az egyik, mint a másik?” kérdésre válaszoló
függvényt. Hanem egy olyat, amelyik egy leképezést ad meg: minden rendezendő elemhez hozzárendel egy értéket, és a rendezés utána
azon értékek szerint történik.
szavak = ["körte", "alma", "dió", "cseresznye"]
szavak.sort()
print(szavak) # alma, cseresznye, dió, körte
szavak.sort(key=len)
print(szavak) # dió, alma, körte, cseresznyeAz első esetben a szavakat rendezzük. Alapértelmezés szerint a .sort() függvény magukat az
elemeket hasonlítja össze. Sztringeknél a növekvő sorrend, a < b ábécé szerinti összehasonlítást jelent,
így kapjuk meg sorban az A, C, D és K betűvel kezdődő szavakat.
szavak[i]
|
|---|
| alma |
| cseresznye |
| dió |
| körte |
szavak[i] | len(szavak[i])
|
|---|---|
| dió | 3 |
| alma | 4 |
| körte | 5 |
| cseresznye | 10 |
A második esetben a rendezéshez kulcsot adunk, és ez a len függvény. Ezért minden egyes
rendezendő elemre a rendezőalgoritmus meghívja a len()-t, pl. len("dió"), len("alma") és
így tovább. Ezzel egész számokat kap, a rendezendő sztringek hosszát, és végülis ezek alapján teszi őket sorba. A sor elejére
a legrövidebb szó kerül (mert ahhoz tartozott a legkisebb szám), a végére pedig a leghosszabb.
A sorted() függvény ugyanígy működik, azzal a különbséggel, hogy az nem módosítja a listát,
hanem új listát ad.
Lássunk példákat rendezések kulcsaira!
class Tort:
...
def tort_valos(t):
return t.szaml / t.nev
tortek = [ ... ]
tortek.sort(key=tort_valos)Az első példa egy racionális szám osztályt mutat. A törteket növekvő sorba szeretnénk rendezni. Ehhez kell egy olyan kulcsot
keresni, minden törthöz egy olyan hozzárendelhető értéket, amik szerint, ha a törteket sorba rakjuk, akkor azok éppen növekvő sorban
lesznek. Egy osztással meghatározhatjuk, hogy az adott tört hol van a számegyenesen (float típusúként ábrázolva a
számot, ha esetleg pontatlanul is) – eszerint rendezve épp kialakul a növekvő sorrend.
Sok apróságot lehetne mutatni ebben a témában, amelyekbe nem megyünk bele részletesen. Az első ilyen dolog az, hogy a rendezés kulcsa lehet az osztály egyik tagfüggvénye vagy operátora is.
Ha a törtünknek amúgy is írtunk __float__ operátort, akkor akár azt is megadhatjuk paraméterként. Ebben az esetben
persze ki kell írnunk az osztály nevét:
class Tort:
...
def __float__(self):
return self.szaml / self.nev
tortek = [ ... ]
tortek.sort(key=Tort.__float__)Lássunk egy másik példát, egy névsort!
class Ember:
def __init__(self, nev, szuletesnap):
...
def ember_szuletesnap(e):
return e.szuletesnap
nevsor = [ ... ]
nevsor.sort(key=ember_szuletesnap)Ha születésnapok szerint szeretnénk rendezni a névsor tagjait, akkor a rendezés kulcsa az egyes objektumok
szuletesnap nevű adattagja. Ezért írunk egy függvényt, amelyik megkapja paraméterként az adott embert, és visszatér
annak születésnapjával.
Szintén csak érdekességként említjük, hogy az egyszerű kis függvény, amelyik megadta egy ember születésnapját, megírható
egy ún. lambda függvényként is. Ez egy névtelen, ad-hoc, egy sorból álló függvény, amit helyben megadhatunk
a paraméternél:
class Ember:
def __init__(self, nev, szuletesnap):
...
nevsor = [ ... ]
nevsor.sort(key=lambda e: e.szuletesnap)A lambda függvényt a lambda e: e.szuletesnap kifejezés adja meg. Ez egyenértékű azzal, mintha megírtuk volna külön
a fenti ember_szuletesnap() függvényt. Csak itt elmarad a függvény neve. Meg a return utasítás is, mert
az egész függvény egyetlen egy kifejezésból állhat, ami most az e.szuletesnap. Ennek az egyetlen kifejezésnek az
értéke lesz a függvény értéke.
Emlékezzünk vissza egy pillanatra az állapotgépekre! Az állapotgépeknél egy adott esemény és az előző események alapján kialakult állapot alapján választottunk mindig ki egy tevékenységet és egy új állapotot. Ezeket kiolvashattuk egy táblázatból is, amely egy kétdimenziós lista volt, amelynek sorait és oszlopait épp az esemény és az állapot segítségével választottuk ki (indexeltük).
Az állapotot könnyű volt eltárolni, mert minden állapothoz egy egész számot rendeltünk hozzá. Az előbb megismert generikus algoritmusok ötlete alapján könnyen betehetjük a táblázatba a tevékenységeket is. Hiszen nincs más dolgunk, mint az egyes tevékenységeket megfogalmazni függvények formájában, és azokat betenni egy táblázatba.
Vegyük példának az „ly” számlálót! Annál a tevékenységek háromfélék lehettek: 1) nincs teendő (nem növeljük a számlálót, 2) eggyel növeljük a számlálót, 3) kettővel növeljük a számlálót. Az állapotgép megtervezése után ezt az állapotátmeneti és tevékenységtáblát kaptuk:
| l | y | egyéb | |
|---|---|---|---|
| alap | →l_volt | - | - |
| l_volt | →ll_volt | sz += 1, →alap | →alap |
| ll_volt | - | sz += 2, →alap | →alap |
Az alábbi kódban létrehozzuk a főprogram lokális változójaként a számlálót, és szintén a főprogram belsejében definiáljuk a három tevékenységet is függvényként. Ezek látni fogják a számláló nevű változót:
def main():
szaml = 0
def nop():
pass
def egy():
nonlocal szaml
szaml = szaml + 1
def ketto():
nonlocal szaml
szaml = szaml + 2
allapotgep = [
[(L_VOLT, nop), (ALAP, nop), (ALAP, nop)],
[(LL_VOLT, nop), (ALAP, egy), (ALAP, nop)],
[(LL_VOLT, nop), (ALAP, ketto), (ALAP, nop)],
]
while True:
# ...
(ujallapot, tevekenyseg) = allapotgep[allapot][kar]
tevekenyseg()
allapot = ujallapotAz állapotgép megvalósítása így egyetlen apró ciklusból áll. A ciklus minden bekövetkező esemény (itt: beérkező karakter) hatására megindexeli a táblázatot, és kiolvassa belőle a tevékenységet és az állapotátmenetet. Ezek után két dolga van:
- Elvégezni a tevékenységet, ami itt a táblázatból kiolvasott függvény meghívásából áll:
tevekenyseg(). - Elvégezni az állapotátmenetet, ami az állapotváltozó felülírásával megvalósítható:
allapot = ujallapot.
Ezekhez minden adat rendelkezésre áll a táblázat egy cellájában, ami egy tuple.
A tevékenységek függvényeiben egy apró dologra figyelni kell. Nevezetesen arra, hogy jelezzük a Pythonnak ezek belsejében,
hogy egy nem lokális változót szeretnének a függvények módosítani: nonlocal szaml. Erre azért van szükség, mert
a szabály az, hogy a belső függvények az őket tartalmazó külső függvény változóit nem módosíthatják. Különben nem látszana
az x = valami alakú értékadásokon, hogy az x nevű lokális változót szeretnék létrehozni, vagy
a külső függvény x nevű változóját írnák felül. Persze ezt megoldhattuk volna úgy is, hogy a számlálót, esetleg
az állapotgép működéséhez tartozó további adatokat egy objektumba tesszük.
A teljes, így megvalósított program letölthető innen: lyszaml_func.py.
Feladat: tegyük egy sakktáblára nyolc királynőt úgy, hogy ne üssék egymást!
| ♛ | |||||||
| ♛ | |||||||
| ♛ | |||||||
| ♛ | |||||||
| ♛ | |||||||
| ♛ | |||||||
| ♛ | |||||||
| ♛ |
Húzd az egeret a királynők fölé!
Lőjünk le néhány kérdést előre! Első kérdésünk lehet, hogy van-e megoldás. A válasz: van, de ez a rajzról is kiderül.
Második pedig, hogy hány megoldás van – összesen 92, amiből csak 12 lényegesen különböző van (a többi forgatással vagy tükrözéssel átvihető egymásba). A programunkban most az összeset megkeressük majd, nem csak a lényegesen különbözőeket; megszámláljuk és ki is rajzoljuk a megoldásokat.
A harmadik kérdésünk az, hogy a feladat általánosítható-e: 9×9-es sakktáblára 9 királynő, vagy 7×7-esre 7 darab. A válasz erre is az, hogy igen. A 2×2-es és 3×3-as esetben nincs megoldás, az összes többi esetben van. A lehetséges megoldások száma igen gyorsan nő a tábla méretével, nagyjából exponenciálisan. 27×27-es táblára
234 907 967 154 122 528
elrendezést találhatunk – lásd a Wikipédia Nyolckirálynő-probléma szócikkét. Ez egyébként a legnagyobb tábla, amire sikerült meghatároznia a megoldások számát egy csapatnak 2016 szeptemberében; nagyobb táblákra a megoldások száma ismeretlen.
Próbáljuk végig a lehetséges megoldásokat!
Ehhez el kell tárolnunk, hogy melyik királynő hol van. Definiáljunk egy pozíció nevű típust, és hozzuk létre belőle a 8 elemű listát!
class Pozicio:
def __init__(self, x, y):
self.x = x
self.y = ykiralynok = [
Pozicio(1, 5),
Pozicio(7, 6), ...
]Hány megoldást kell végigpróbálnunk?
Hány megoldást kell végigpróbálnunk? Összesen 8×8 = 64 mezőre kell 8 királynőt raknunk. Vagyis 64 mezőből 8-at kell választanunk, ahol lesz királynő, a többi mezőkön nem. Ez ugyanaz a probléma matematikailag, mint a lottósorsolás, ahol 90 számból kell 5 különbözőt választani. A kombinatorikában ezt ismétlés nélküli kombinációnak nevezik. Ezek számát, „64 alatt a 8-at” jópár faktoriális kiszámításával lehet meghatározni:
64!
C = ──────────── = 4 426 165 368
8!·(64-8)!
100 000 próbálkozás / másodperc → 44 261 másodperc → fél nap.
Ha a gépünk százezer állást tud végigpróbálni másodpercenként, akkor is fél napig fog futni a programunk. Ezért másképp kell okoskodni, még akkor is, ha valójában a mai asztali számítógépek sokkal gyorsabbak ennél (kb. 1–10 millió próbálkozás / másodperc is belefér).
| 5 | ♛ | |||||||
|---|---|---|---|---|---|---|---|---|
| 2 | ♛ | |||||||
| 4 | ♛ | |||||||
| 7 | ♛ | |||||||
| 3 | ♛ | |||||||
| 8 | ♛ | |||||||
| 6 | ♛ | |||||||
| 1 | ♛ |
Mivel nem lehet egy sorban két királynő (ütnék egymást vízszintesen), ezért biztosak lehetünk abban, hogy
minden sorban pontosan egy királynő lesz (8 sor, 8 királynő). Tehát lényegében elég csak azt megmondanunk a programunkban, hogy
melyik sorban hol van a királynő. És ezt eltárolni is bőven elegendő; egy 8 elemű, int-eket tartalmazó listára van
csak szükségünk. Ha például poz[3] == 7, az azt jelenti, hogy a harmadik sor királynője a hetedik oszlopban van.
Észrevehetjük, hogy minden sorban pontosan egy királynő lesz:
poz = [5, 2, 4, ...]Hogyan számítjuk ki így a végigpróbálandó esetek számát? A tömbelemek a 0...7 (1...8) értékeket vehetik fel. Ez 8n lehetőséget jelent, ahol n a tömbelemek száma; az pedig most szintén 8. A kombinatorikában ez az ún. ismétléses variáció.
V = 88 = 16 777 216
Vagyis 16,7 millió esetről van szó – az előzőek 260-adrészéről. Ez már sokkal inkább vállalhatónak tűnik, de még valamit észre kell vennünk.
Kétszer nem szerepelhet ugyanaz a szám:
poz = [1, 2, 3, 4, 5, 6, 7, 8]Ha a listában kétszer szerepelne ugyanaz a szám, az azt jelentené, hogy két különböző királynő ugyanabban az oszlopban van. Akkor viszont ütnék egymást függőlegesen, ezért ezeket az eseteket is kizárhatjuk. Vagyis valójában nem egy ismétléses variációt keresünk, hanem a fenti, 1-8 számokat tartalmazó lista permutációit. Az tehát a kérdésünk, hogy ennek a listának mely keverései, sorbaállításai adják a megoldást.
P = 8! = 40 320 !
A permutációk száma faktoriálissal határozható meg. A 8-elemű tömbünk lehetséges permutációinak száma 40320, vagyis az eredetileg kigondolt 4,4 milliárd megvizsgálandó esetet százezred részére tudtuk csökkenteni! Ha ez még nem lenne elég, az így kialakított listában az ütési helyzetek vizsgálata is egyszerűbb. Mivel eleve minden sorba csak egy királynőt rakunk (a sor száma az index), és minden oszlopba is egyet (a listaelemek egymástól különböző értékei), így már csak az átlós ütéseket kell vizsgálnunk majd, a függőlegeseket és a vízszinteseket nem.
Ütésben vannak, ha
Tehát csak az átlós ütésekkel kell foglalkozni. Átlós ütés akkor van, ha ugyanannyi sort kell lépni az egyik királynőtől a másikig, mint ahány oszlopot.
- 45 fokos átlón: dx = dy
- –45 fokos átlón: dx = –dy
- A kettő együtt: |dx| = |dy|
Figyelembe kell vennünk, hogy ez mindkét irányú átlón megtörténhet. De ha vesszük az ugrások abszolút értékét (hogy mindegy legyen, fel vagy le, illetve jobbra vagy balra kell menni), akkor egyetlen egy egyenlettel leírhatjuk, mikor van ütközés: ha |x1–x2| = |y1–y2|.
A vizsgálatot ez a függvény fogja végezni:
def kiralyno_oke(poz):
for i in range(len(poz) - 1):
for j in range(i + 1, len(poz)):
if abs(poz[i] - poz[j]) == abs(i - j):
return False
return TrueAz adatszerkezetünkben a tömbindexek a sorok, a tömbértékek pedig az oszlopok. Vagyis ha bármely két tömbelemre igaz az, hogy az indexek különbsége megegyezik az értékek különbségével, akkor ütést találtunk, és az nem megoldás. Ha sehol nincs ilyen, akkor a tömb egy helyes megoldást tartalmaz.
Valójában az abs(i - j) helyett írhattunk volna j - i-t. A j index
mindig nagyobb, mint az i (ez látszik a ciklushatárokon), tehát így biztosan pozitív számot kapnánk, abszolút érték
nélkül is. A fenti példakódban maradt az abs(i - j), mert jobban illeszkedik a gondolatmenethez.
Ha ezek megvannak, a megoldások előállítása a permutációk végigpörgetéséből, és azok vizsgálatából áll.
A permutációk előállítása egy rekurzív algoritmussal történik. A rekurzív algoritmus gondolatmenetét egy négyelemű listán szemléltetjük: [1, 2, 3, 4]. Ennek permutációi négy csoportba oszthatóak:
- [1, x, x, x], az egyessel,
- [2, x, x, x], a kettessel,
- [3, x, x, x], a hármassal,
- [4, x, x, x], a négyessel kezdődő permutációk.
Az x-szel jelzett helyeken pedig a többi elem van. A többi elemet szintén sorba lehet rakni különféle módokon. Pl. a [1, x, x, x] esetben ezek a [2, 3, 4], amelyek lehetséges sorrendezései: [2, 3, 4], [2, 4, 3], [3, 2, 4] stb. Ezek pedig előállíthatók rekurzívan, hiszen itt egy háromelemű lista permutációit keressük.
A permutációk előállításának algoritmusa tehát az alábbi:
Permutáció
- Menjünk végig a sorozaton. Tegyük mindegyik elemét az elejére.
- Az így kapott sorozat fennmaradó részét permutáljuk.
- Tegyük vissza az elemet a helyére.
Másképp fogalmazva: előreveszünk egy elemet, kavargatjuk a többit. Aztán előreveszünk egy másik elemet, és megint kavargatjuk a többit. Ezt kell megcsinálni mindegyik elemmel.
def permutal(lista, honnan=0):
if honnan == len(lista): # !
print(lista)
return
for i in range(honnan, len(lista)):
csere(lista, honnan, i)
permutal(lista, honnan + 1) # !
csere(lista, honnan, i)A rekurzív hívásban mindig csak a lista fennmaradó részét kell permutálni, ezért a lista mellett átveszünk
egy honnan nevű paramétert is. A cserék innen indulnak, a rekurzív hívásban pedig honnan + 1
lesz a következő paraméter (a fennmaradó rész). Amikor eljutunk a honnan == meret értékig, akkor előállt
egy permutáció, tehát ez a báziskritérium. Úgy jutottunk oda, hogy közben valamilyen sorrendbe át lett rendezve
a számsor, ezért a programnak abban a pontjában használhatjuk fel az eredményt – jelen esetben csak kiírjuk a számsort.
A rekurziót honnan = 0-val kell indítani; ezt legegyszerűbb úgy megoldani, hogy annak a paraméternek
egy alapértelmezett értéket adunk. Így a permutal(szamsor) hívás lehetséges, és permutal(szamsor, 0)-t
jelent.
Látható, hogy a ciklus az első iterációban nem cserél semmit; akkor épp i == honnan a ciklusváltozó értéke.
Gyakran azt a kódrészletet így szokás írni, hogy ne cserélje meg saját magával feleslegesen a listaelemet:
permutal(lista, honnan + 1)
for i in range(honnan + 1, len(lista)):
csere(lista, honnan, i)
permutal(lista, honnan + 1)
csere(lista, honnan, i)De jelen esetben ennek nincs jelentősége.
Ha ez megvan, nincs más teendőnk: az előálló permutációkat megvizsgálni, és csak az elfogadhatóakat kirajzolni.
def kiralyno_keres(poz, honnan=0):
if honnan == len(poz):
if kiralyno_oke(poz): # !
kiralyno_kiir(poz)
return
for i in range(honnan, len(poz)):
csere(poz, honnan, i)
kiralyno_keres(poz, honnan + 1)
csere(poz, honnan, i)
def main():
kiralyno_keres([1, 2, 3, 4, 5, 6, 7, 8])Az elkészült program letölthető innen: 8kiralyno_perm.py.
| 1 | ♛ | |||||||
|---|---|---|---|---|---|---|---|---|
| 2 | ♛ | |||||||
| ? | ||||||||
| ? | ||||||||
| ? | ||||||||
| ? | ||||||||
| ? | ||||||||
| ? |
Valójában most is rengeteg feleslegesen kipróbált megoldás van:
poz = [1, 2, ???]
poz = [3, 2, ???]
poz = [1, ?, 3, ???]
poz = [6, ?, 4, ???]A permutációs módszerrel rengeteg állást megvizsgáltunk hiábavalóan. Például az első királynőt leraktuk az első oszlopba, a másodikat a második oszlopba (mint a rajzon). Ezek biztosan ütik egymást, tehát a maradék hatot hiába próbáljuk meg elhelyezni bárhogyan, helytelen lesz a megoldásunk. A maradék 6 királynő elhelyezésére 6! = 720 lehetőség van, tehát ennyi állás vizsgálatát kihagyhattuk volna. És nem ez az egyetlen ilyen eset; a fenti listakezdemények mind olyan elhelyezéseket mutatnak, ahol a kérdőjelek helyére bármi is kerül, biztosan rossz a megoldás.
Tehát a nyolckirálynő-problémában:
- Részmegoldások vizsgálhatók (első n sor).
- Ezek vizsgálatával sok lehetőség kizárható.
Vannak olyan feladványok, ahol egy lehetséges megoldást egyben kell látnunk, és csak akkor tudjuk eldönteni, hogy helyes-e. A nyolckirálynő-probléma azonban nem ilyen. Itt egy részmegoldást is tudunk vizsgálni. Vagyis egy még nem teljesen kitöltött táblára kétféle állítást tehetünk, a) ez még lehet jó, próbáljuk meg kitölteni az alját, b) ez már biztosan nem lesz jó. Vagyis hasznos megvizsgálnunk a részmegoldást is, mert az ki fog zárni egy csomó esetet.
Az algoritmus működése:
- Tekintsük a következő üres sort.
- Próbáljuk végig az összes oszlopot a sorban.
- Tegyük a táblára a királynőt.
- Ha üti az eddigieket, vegyük le.
- Ha nem üti, akkor:
- Próbáljuk elhelyezni a többit.
- Végül vegyük le, a többi oszlopot is próbáljuk.
- Ha közben megtelik a tábla, megoldást találtunk.
A kiemelt műveleteket („ha üti, vegyük le”) nevezzük visszalépésnek, ezért az algoritmus neve: visszalépő keresés (backtracking search).
Az új algoritmushoz egy egyszerűbb tesztelőfüggvény tartozik, mint az előzőhöz. Mivel most egyesével rakjuk majd a királynőket, mindig csak a legutóbbit kell megnézni, hogy jó-e, nem üti-e a többit. Az összes előzőre nem figyelünk: úgy jutunk mindig ide, hogy azok már ellenőrizve vannak.
Ütésben vannak, ha
- Azonos oszlopban vannak: x1 = x2
- Azonos átlón vannak: |dx| = |dy|
Ebben az algoritmusban feltételezzük, hogy a lista nem annyi elemet tartalmaz, amilyen magas a tábla, hanem csak az első valahány darab királynőt, amit már feltettünk a táblára. Vagyis a legutolsó elem az, amit vizsgálunk.
def kiralyno_utolso_oke(poz):
utso = len(poz) - 1
for i in range(utso):
if (poz[i] == poz[utso]
or abs(poz[i] - poz[utso]) == abs(i - utso)):
return False
return TrueÜgyelni kell arra, hogy most nem csak az átlót kell vizsgálni, hanem azt is, hogy az új királynő nem került-e
valamelyikkel azonos oszlopba: poz[i] == poz[utolso]. A listába ugyanis most nem permutációk kerülnek, hanem minden
sorban végigpróbáljuk az összes oszlopot, és oszlopok szerinti ütés is előfordulhat. De ez csak egy újabb feltétel; az algoritmus
még így is egyszerűbb, egyetlen egy ciklus vizsgálja az új királynő sora előtti sorokat.
Az alábbi függvény valósítja meg a visszalépő keresést a probléma megoldására. Ez nem a klasszikus megvalósítás, még később finomítjuk majd, de előbb lássuk a működését!
A függvénynek paramétere most a mekkora nevű változó, amelyik azt mutatja, hogy mekkora
játéktáblán kell megtalálni a megoldásokat. Ugyanis most egy teljesen üres listából indulunk ki, ahogy a hívásnál is látszik.
def kiralyno_keres(poz, mekkora):
if len(poz) == mekkora:
kiralyno_kiir(poz)
return
for uj in range(1, mekkora + 1):
poz.append(uj)
if not kiralyno_utolso_oke(poz):
poz.pop() # visszalépés
continue
kiralyno_keres(poz, mekkora)
poz.pop()
def main():
kiralyno_keres([], 8)A ciklus megpróbálja elhelyezni az új királynőt. Ez végigpróbálja 1-től 8-ig a lehetséges értékeket,
amelyek abba a listaelembe kerülhetnek, vagyis a lehetséges oszlopokat. Az a hipotézis, hogy az új oszlop a királynő számára jó
lesz, ezért be is teszi oda: poz.append(uj). Utána pedig megnézi, hogy a hipotézis jó-e. A
kiralyno_utolso_oke() függvénynek ezt az egy új királynőt kell néznie, mivel az összes eddigi biztosan nem üti
egymást. Ha kiderül, hogy ez ütésben van az eddigiekkel, akkor kiveszi a listából: poz.pop(), és próbálkozik tovább.
Ha rendben van, akkor pedig a rekurzív hívással megpróbálja elhelyezni a többit.
Lényegében az .append() és .pop() függvényhívásokkal egy veremnek használjuk a listát, mert mindig a
végére teszünk új elemet, és onnan is törlünk.
A feltétel tagadásával természetesen egyszerűbb kódhoz lehetne jutni (látszik, hogy akár jó volt az új helyen a királynő, akár nem, mindenképp kivesszük a listából). De így jobban követhető a keresés logikája. A letölthető változatban a rövidebb megoldás szerepel: 8kiralyno_bt.py.
Az előbbi magyarázatban a visszalépő keresés tisztázása kedvéért szerepelt egy egyszerűsítés: ismétléses variációkat vizsgáltunk, nem pedig permutációkat. Vagyis nem az [1, 2, 3, 4, 5, 6, 7, 8] listát permutáltuk, hanem minden sorban az összes oszlopba próbáltunk királynőt tenni.
Valójában a permutációkat előállító algoritmus beilleszthető a visszalépő keresésbe. Vegyük szemügyre csak a permutációkat előállító kódot egy pillanatra! Ez így fest:
def permutal(lista, honnan):
if honnan == len(lista):
return
for i in range(honnan, len(lista)):
csere(lista, honnan, i)
permutal(lista, honnan + 1)
csere(lista, honnan, i)Ebben a cserékkel minden listaelem előre jön, utána a rekurzióban csak a lista fennmaradó részét permutáljuk. A nyolckirálynő-probléma és a visszalépő keresés esetében ez éppen jó nekünk: a cserével előre hozott szám (oszlop index) lesz a vizsgálandó elem a báziskritériumban. Ha az rendben van, akkor a lista végét permutáljuk utána csak, vagyis csak ott rendezgetjük a királynőket; az eddig elhelyezettek között az újak miatt már nem lesz ütközés.
def kiralyno_keres(poz, n=0):
if not kiralyno_nedik_oke(poz, n - 1): # !
return
if n == len(poz):
kiralyno_kiir(poz)
return
for i in range(n, len(poz)):
csere(poz, n, i)
kiralyno_keres(poz, n + 1)
csere(poz, n, i)
def main():
kiralyno_keres([1, 2, 3, 4, 5, 6, 7, 8])A végleges megoldásunk tehát ez. Valójában ez alig különbözik az első, permutáló megoldástól. Az egyetlen különbség abban rejlik, hogy ez részmegoldásokat is megvizsgál, és azokat nagyon hamar visszautasítja, ha nem jók. Ezt mutatja a felkiáltójellel jelölt rész: ez a visszalépés.
A teljes program letölthető innen: 8kiralyno_bt_perm.py.
Az alábbi táblázat azt mutatja, hogy táblaméret függvényében hány pályaállást kell megvizsgálni akkor, ha a teljes permutációkat előállító módszert, illetve a visszalépő keresést alkalmazzuk a probléma megoldására.
| méret | permutációval | visszalépővel | gyorsulás |
|---|---|---|---|
| 8 | 40320 | 5509 | 7,3× |
| 9 | 362880 | 24012 | 15,1× |
| 10 | 3628800 | 110005 | 33,0× |
| 11 | 39916800 | 546358 | 73,1× |
| 12 | 479001600 | 2915741 | 164,3× |
| 13 | 6227020800 | 16469570 | 378,1× |
| 14 | 87178291200 | 99280505 | 878,1× |
Látható, hogy a visszalépő keresés sokkal gyorsabb; a hibás részmegoldások (és azok befejezéseinek) eliminálásával a gyorsulás a táblamérettel meredeken nő. 14×14-es tábla megoldásainak keresésekor már majdnem 900-ad részére csökken a megvizsgált esetek száma.
Ez az algoritmus azért is sokkal gyorsabb, mert az egyes esetek vizsgálata egyszerűbb. Míg a permutáló algoritmusnál teljes játékállásokat kellett vizsgálni (minden királynőt mindegyikkel párba állítva), itt egy hipotézis vizsgálatához elég csak az újonnan felrakottat figyelembe venni. Egy i5-8250U processzorral rendelkező gépen a 13×13-es pályára a megoldások megkeresése mindössze 30 másodpercig tart.
Lent látható a visszalépő keresés általános megfogalmazása pszeudokód formájában. Ez annyiban különbözik az előbb látott nyolckirálynő-megoldótól, hogy itt a hipotézis helyességének a vizsgálata is báziskritériumként szerepel. Vagyis a ciklus feltétel nélkül elindítja a rekurziót a kiegészített megoldás vizsgálatára; aztán a rekurzív hívás dönti el, hogy elfogadja vagy visszautasítja azt a megoldást, amit éppen lát.
függvény: visszalépő_keresés(megoldás)
ha a (rész)megoldás hibás báziskritériumok
vissza
ha megoldás elfogadható
kiírás
vissza
ciklus a következő részmegoldásokkal egyszerűsítés
megoldás kiegészítése
visszalépő_keresés(megoldás)
A fenti algoritmus az összes megoldást kilistázza. De a visszalépő keresés könnyedén módosítható olyan feladatok megoldására, ahol csak egy megoldást keresünk, vagy esetleg meg akarunk állni az első egynéhány megoldás megtalálása után.
Ha egy megoldás keresése a feladat, akkor ahhoz bevezetünk a függvénynek egy visszatérési értéket. Ez fogja azt mutatni, sikerült-e megoldást találni vagy nem.
def kiralyno_keres(poz, n=0):
if not kiralyno_nedik_oke(poz, n - 1):
return False # !
if n == len(poz):
return True # !
for i in range(n, len(poz)):
csere(poz, n, i)
if kiralyno_keres(poz, n + 1):
return True # !
csere(poz, n, i)
return False # !def main():
poz = [1, 2, 3, 4, 5, 6, 7, 8]
talalt = kiralyno_keres(poz)
if talalt:
kiralyno_kiir(poz)Ha True értéket kapunk a függvényből, akkor sikerült egy megoldást találni, és az a listában van.
Ha False, akkor nem volt megoldás, és a listában nincs hasznos adat.
A függvény belsejében elő kell állítani ezt az értéket. Egyrészt a báziskritériumoknál: ha rossz helyre került a királynő,
akkor False, ha elértük a tábla végét, akkor jó helyen vannak, és True.
Másrészt pedig magában a keresésben. A leglényegesebb rész az, ahol a rekurzív hívás van. Ha az igazzal tér vissza, azt azt jelenti, hogy a lista egy teljes megoldást tartalmaz; ilyenkor a hívó is visszatér igazzal. Ez az, ami megszakítja a keresést az első megoldás megtalálása után, ugyanis ilyenkor megáll egyrészt a ciklus is, másrészt pedig a rekurzív hívók is mind igazzal fognak visszatérni. A függvény legalján pedig hamis értékkel kell visszatérni. Ugyanis ha lefutott a ciklus teljes egészében, az azt jelenti, hogy a szóba jövő oszlopok közül egyik se vezetett megoldáshoz.
Így működik a rekurzió kapcsán bemutatott labirintus megoldó is. Ott tudjuk előre, hogy egyetlen egy megoldás van, és azt kell megtalálni; zsákutca esetén pedig visszajönni.
A visszalépő keresés alkalmazásai:
- Rejtvények: nyolc királynő, sudoku, keresztrejtvény, labirintus
- Nyelvi elemzés (fordítóban)
- Optimalizálási feladatok, pl. hátizsák-probléma, pénzosztás

Lássunk néhány példát a visszalépő keresés alkalmazására!
Nyelvi elemzés. A fordítóprogramnak a megkapott forráskódot elemeznie kell, és az elemzés közben könnyen zsákutcába
futhat. Például az x--y kifejezés értelmezésekor rá kell jönnie, hogy kerülhet egymás mellé két - karakter.
Ha megpróbálja egy operátorként értelmezni (mint pl. -= is két karakterből áll), akkor zsákutcába jut, Viszont
ha megáll ott, hogy az első - egy kivonás, akkor a második - is kaphat értelmet: ellentettképzésről
van szó. A teljes kifejezés jelentése: x - (-y).
Optimalizálási feladatok. Ezek közül a legismertebb a hátizsák-probléma, amit a rajz is szemléltet. Adott egy hátizsák, amelynek a teherbírása véges. Adott egy csomó tárgy, amelyeknek ismerjük az értékét és a súlyát. Kérdés, mely tárgyakat kell kiválasztanunk, hogy a legnagyobb összértéket állítsuk össze, figyelembe véve a hátizsák teherbírását. A rajz példáját tekintve, a két legértékesebb tárggyal 10+4 = 14 dolláros csomagot állíthatnánk össze, ezeknek a súlya azonban 12+4 = 16 kg, ami túllépi a limitet. Valamelyiket el kell hagynunk, és könnyebbet keresni helyette.
Szintén visszalépő kereséssel oldható meg helyesen egy bankautomata feladata is, amelynek ki kell adnia egy adott összeget, figyelembe véve, hogy milyen címletekből mennyi áll rendelkezésre. Ha a bankautomata rekeszei ezeket a bankjegyeket tartalmazzák:
| címlet | darabszám |
|---|---|
| 5000 | 137 |
| 2000 | 275 |
| 1000 | 0 |
Akkor egy mohó algoritmus, amely a legnagyobb címletekkel próbálkozik a 6000 forint kifizetéséhez nem tudna megoldást találni. Elakadna ott, hogy ad egy 5000-est, és utána 1000-esből meg nincsen. Viszont ezen a ponton visszalépve, úgy döntve, hogy mégsem ad ki 5000-est, rájöhet, hogy a 3×2000 megoldása a feladatnak.